Random Boolean Nets and Features of Language

James R Hurford,
Language Evolution and Computation Research Unit,
Linguistics Department, University of Edinburgh

Abstract

This paper describes an attempt to cast several essential, quite abstract, properties of natural languages within the framework of Kauffman's random Boolean nets. These properties are: complexity, interconnectedness, stability, diversity, and underdeterminedness. Specifically, in the research reported here, a language is modelled as an attractor of a Boolean net. (Groups of) nodes in the net might be thought of as linguistic principles or parameters as posited by Chomskyan theory of the 1980s. According to this theory, the task of the language learner is to set parameters to appropriate values on the basis of very limited experience of the language in use. The setting of one parameter can have a complex effect on the settings of other parameters. A random Boolean net is generated and run to find an attractor. A state from this attractor is degraded, to represent the degenerate input of language to the language learner, and this degraded state is then input to a net with the same connectivity and activation functions as the original net, to see whether it converges on the same attractor as the original. In practice, many nets fail to converge on the original attractor, and degenerate into attractors representing complete uncertainty. Other nets settle at intermediate levels of uncertainty. And some nets manage to overcome the incompleteness of input and converge on attractors identical to that from which the original inputs were (de)generated. Finally, an attempt was made to select a population of such successful nets, using a genetic algorithm, where fitness was correlated with an ability to acquire several different languages faithfully. It has so far proved impossible to breed such successful nets, lending some plausibility to the Chomskyan suggestion that the human language acquisition capacity is not the outcome of natural selection.

The advantage of putting these two sets of ideas together is that it relates the Chomskyan picture to a model whose properties are somewhat well understood, and which, moreover, is simple enough and well specified enough to lend itself to computational implementation. No empirical claims are made, but the hope is that readers who have previously understood one, but not the other, of the two sets of ideas juxtaposed here will be able to see the formerly unfamiliar framework (whichever one it is) in a new and illuminating light.

In the first two sections, the two sets of ideas are sketched separately; the third section gives an interpretation of random Boolean nets in terms of knowledge, acquisition, and transmission of language.

What aspects of language to model?

Consider the following six striking (yet uncontroversial) features of natural languages.

• complexity
• interconnectedness
• fidelity of transmission
• stability
• diversity
• learnability from incomplete data

We will briefly discuss each of these features in turn.

Complexity. Each human language is an extremely complex system. No complete grammar of any language has ever been written. One of the largest grammars of English, (Quirk et al., 1972), which is 1102 pages long, is still incomplete in detail.

Linguists are still constantly finding subtle and complex patterns of behaviour/judgement, even in English, the most-studied language, thatstubbornly resist encapsulation in any theoretical framework. This is the stuff of syntacticians' journal articles.

Interconnectedness. The idea that ``Une langue est un systeme ou tout se tient'' [``A language is a system in which everything holds onto everything else''] is such a hoary truism that its origins are lost in the mists of linguistic historiography¹.

The interconnectedness of facts in a language shows itself in many ways. From opposite ends of the theoretical linguistic spectrum, both Greenbergian conditional universals and Chomskyan parameters exemplify this interconnectness.

• Greenbergian conditional universals:
  • If a language has a dual, it also has a plural;
    (A dual is a marker, typically a suffix, on a noun indicating exactly a pair of things, e.g. Arabic rigleen [rigl = `leg', -een = dual] `two legs'; an example of a plural marker is the English s suffix as in legs}.)
  • If a language is SOV, it has postpositions;
    (An SOV language is one with the basic word order subject-object-verb, as in Turkish or Japanese; a postposition is a word with a similar meaning to a preposition (such as English on), but which follows its noun.)
  • If a language is VSO or SVO and has prepositions, it puts the relative clause after the noun.
    (A VSO language is one with the basic word order verb-subject-object, as in Celtic languages or Classical Arabic; an SVO language is one whose basic word order is subject-verb-object, as in English or Colloquial Arabic.)
• Chomskyan parameters:
  • Pro-drop: If a language allows null subjects,
    • it allows inverted verb-subject order in declaratives,
    • it has no `expletives' such as it and there,
    • it has morphologically uniform verbal inflectional paradigms.

Fidelity of transmission. The English of 100 years ago is still intelligible now. In a community not subject to social upheaval, the differences between the language of one generation and the next are minimal.

Stability. An individual's language behaviour and linguistic judgements vary only slightly over time (again, in a community not subject to social upheaval).

Diversity. There are about 6000 different languages in the world, mutually unintelligible. Putting aside vocabulary differences, probably no two languages have exactly the same grammatical system. Chomsky suggested that the number of grammatically distinct possible languages is finite. ``When the parameters of UG are fixed, a core grammar is determined, one among finitely many possibilities, lexicon apart.'' (Chomsky, 1981:137)

Learnability from incomplete data. A newborn child can learn any language perfectly. The well-known `Poverty of Stimulus' argument states that the knowledge of language (in the form of solid intuitions of wellformedness) possessed by adults is underdetermined by the examples to which they were exposed as children. The question provoked by this has been referred to as `Plato's Problem', and expressed as ``how can we know so much on the basis of so little experience?''

The data to which the language-acquiring child is exposed are susceptible to infinitely many generalizations, most of which our linguistic intuitions immediately dismiss as far-fetched. Indeed it is precisely the solidity of many of these intuitions that seems to prevent some students from seeing the point of the poverty of stimulus argument and its implication for the innateness of certain general facts of grammar. A typical example involves the formation of interrogative sentences in English, in which the first auxiliary verb of the main clause is `moved' around to the front of the subject of the sentence, as in:

The fact that it is raining should deter us.
Should the fact that it is raining deter us?

But not

*Is the fact that it raining should deter us

In the ungrammatical example, the first auxiliary verb in the string, is, has been moved incorrectly to the front of the sentence. We know that this is wrong; but how do we know? It cannot be just from example, because most of the examples that we hear are equally compatible with the hypothesis that interrogatives are formed by moving the first auxiliary verb in the string.

Summaries of the Poverty of Stimulus argument can be found in many introductory texts on syntactic theory (e.g. Cook and Newson, 1996:81-85); there are many more advanced discussions of it in the literature (e.g. Chomsky, 1980; Crain, 1991; Garfield, 1994; Wexler, 1991). For counterargument, see Sampson (1997:38-45).

Random Boolean Networks

A Boolean network can be described in terms of its nodes, connections, activation functions, and states We will introduce these briefly in turn.

Nodes: The number of nodes in a net is expressed conventionally by the variable N. (N = 10, ... , 1000, ... 1000000, ... ) Nodes are set to bit values --- {0,1}. Each node is assigned a (random) Boolean activation function (see below).

Connections (unidirectional) between nodes: Each node takes input from some specified number of other nodes. The number of connections leading into a node is conventionally expressed by the variable K. In a net, all nodes may take the same number of inputs, (K = 2, 3, 4, ... ), or, a possibility less often explored, varying numbers of inputs.

Activation functions: Nodes are activated by Boolean functions of the values of the nodes inputting to them. For a node with K inputs, there are 2^(2K) possible Boolean activation functions. For example with 1 input, possible functions are `FALSE' (00), `COPY' (01), `NEGATE' (10), or `TRUE' (11), as shown in the table below:

Input	`FALSE'	`COPY'	`NEGATE'	`TRUE'
0	0	0	1	1
1	0	1	0	1

States: The state of a network at a given time is the set of its node-settings. There are 2^N possible states of a net.

Boolean networks are dynamic. They are set in motion by the following steps.

• INITIALIZE: set all the nodes in a net to arbitrary binary values.

• RUN: Simultaneously update the values of all nodes according to their inputs from other nodes and their activation functions.

• REPEAT the previous step until the net is in a state it has already been in once before. From this point, the net will cycle repeatedly around a finite set of states.

Boolean networks have attractors. The set of states around which a net cycles repeatedly is an attractor. A given net may have many different attractors, depending on its initial state. An attractor is also called a ``limit cycle''.

Boolean networks have basins of attraction. The set of states from which a net will always end up in a particular attractor is that attractor's basin of attraction. An attractor is a subset of its basin of attraction (typically a proper subset).

Here are some simple examples, where N = 20, and K = 2, with connections and activation functions chosen randomly:

STEP
1	[0	1	0	0	0	1	0	0	0	1	0	0	1	0	1	1	0	1	0	1]
2	[0	1	0	0	0	0	1	0	1	1	0	0	0	1	1	0	0	1	0	1]
3	[0	0	0	0	0	1	1	0	1	1	1	1	1	0	1	0	0	1	0	1]
4	[0	1	1	0	0	1	0	0	1	1	1	1	1	0	1	0	1	1	0	1]
5	[0	1	0	0	0	0	0	0	1	1	1	0	0	0	1	0	1	1	0	1]
6	[0	1	0	0	0	0	0	0	1	1	1	0	0	0	1	0	1	1	0	1]

Here, from the initial random state at step 1, the net has converged on a one-state attractor at step 5: the state at step 5 and all subsequent steps is:

[0

1

0

0

0

0

0

0

1

1

1

0

0

0

1

0

1

1

0

1]

STEP
1	[1	1	0	0	1	1	1	0	1	0	0	0	1	0	1	1	0	0	0	1]
2	[0	0	1	0	0	1	0	1	1	1	1	1	1	0	1	1	0	1	0	0]
3	[1	1	0	0	1	1	1	0	0	0	0	1	1	0	1	0	0	1	1	1]
4	[0	1	1	0	0	1	0	1	0	1	1	1	1	0	1	1	1	1	0	0]
5	[1	1	0	0	1	1	1	0	1	0	0	1	1	0	1	0	0	1	1	0]
6	[0	1	1	0	0	1	0	1	0	1	1	1	1	0	1	1	1	1	0	0]

Here, from the initial random state at step 1, the net has converged on a two-state attractor: the state at step 6 is the same as at state 4. The net will oscillate between the following two states forever.

[0	1	1	0	0	1	0	1	0	1	1	1	1	0	1	1	1	1	0	0]
[1	1	0	0	1	1	1	0	1	0	0	1	1	0	1	0	0	1	1	0]

General Properties of RBNs.

• Where K = 2, the average length of a limit cycle (attractor) is of the order of . For exaple, for N = 100000, the mean length of attractors is 317.
• As K increases,
  • attractors get longer,
  • attractors get fewer.
• In a chaotic regime, attractors are so long that, practically, one never sees the same state twice.
• In a chaotic regime, similar initial states give rise to divergent trajectories through state space.
• Typically (but crucially depending on the activation functions), values of K over 3 induce chaotic regimes.

Interpretation of Nets as Language Knowledge and Language Acquisition

Having set out some basic, though striking, properties of natural languages and outlined the workings of random Boolean nets, I will now suggest a way of interpreting such nets in terms of the linguistic properties mentioned in the first section.

• Particular net states are interpreted psychologically, i.e., as corresponding in some way to an individual's knowledge of his/her language.

• The values of nodes in an attractor state denote (more or less abstract) features of some particular language, e.g.
  • Whether or not it has a case system;
    (A language with case system marks its nouns according to their function in the sentence as subjects, objects or various other functions; Latin, Russian, German and Greek are languages with case systems.)
  • Whether or not it has dual number;
  • Whether or not it is ergative.
    (An ergative language marks the subject of an intransitive sentence with the same marker as the object of a transitive sentence.)
  These language features are binary, a property required by the Boolean character of the model. Features of language which are non-binary can, of course, be coded in a binary fashion.

• Connectivity between nodes is then readily interpreted as linguistic connectedness (dependencies) between features of a language. For example, a node interpreted as indicating whether or not a language permits null subjects could take input from (i.e., be activated as a function of) a node interpreted as indicating whether or not the language has expletives (such as impersonal it and existential there).

• N (the number of nodes) correlates with the complexity of a language. For a reasonable model of a language, N > 10,000 . This, in some sense, is the `number of facts' in the grammar of the language. Given the Boolean network model, where K > 0, none of these facts are independent.

• The connections and activation functions of a net (but not its states) denote properties that the language learner brings to the acquisition task. These, then, model the innately known dependencies between one part of a language and another, the expectations (unconscious, of course) that a human infant has.

• Small attractors denote relative stability. A one-state attractor denotes a speaker's certainty about all features of the language. A two-state attractor denotes uncertainty in the shape of oscillation, for a subset of features, between alternative behaviours or judgements. A very large attractor (limit-cycle) denotes great uncertainty in a speaker. Typically, speakers are quite sure of their judgements about most examples, and their actual behaviour (performance errors aside) is quite consistent. Languages, though complex, are not chaotic.

• Large numbers of distinct attractors denote linguistic diversity. If the same net, starting from different initial states, can reach many different attractors, this models the fact that humans can learn many different languages.

Modifying networks to model acquisition from incomplete primary linguistic data. The language learner is not exposed to examples of all the features of a language, but neverthless acquires them, as mentioned above in connection with the Poverty of Stimulus. We model this as follows:

• The learner's trigger experience of a feature results in a `0' or `1' setting of a node. For example, if a learner hears a clear example of an expletive (e.g., impersonal it), the initial setting of the node containing information about such expletives could be set to a 1 value.
• Without such triggering experience, nodes are set to a `?' value. This model makes an idealizing `single gulp' assumption about the learner's exposure to the primary linguistic data. The presentation of the data is a single operation, putting the net into its initial state. After this triggering by data from outside the net itself, all further activation of nodes is via the internal connections and activation functions of the net.
• Thus a learner net is initialized to a mixed state with {0, 1, `?'} values. The use of `?' values means that there are no default values assumed in the initial state of the net. It would be possible to implement the model with default 0 or 1 values (hence without `?' values), but this possibility has not been explored here.
• In running a net, for all `?' values input to a node, the new value is computed for both 0 and 1 inputs; if in all cases the new value would be the same (either 0 or 1), that value is taken as the new value; otherwise the new value of the node is set to `?'. This makes a very conservative assumption about learning. A node is only set to a non-query value (1 or 0) if all the inputs to it agree on that value.

Applying these ideas, we can give some examples of learning from incomplete data. In the examples below, again N = 20 and K = 2, with randomly chosen connectivity and activation functions. The initial random state contains a number of `?'s, indicating that the learner has experienced no data that would lead to settings of those nodes. We give first an example of unsuccessful learning, in which the net reaches an attractor that still has some nodes set to `?'.

(UNSUCCESSFUL LEARNING)

(SUCCESSFUL LEARNING)

Modelling adult-to-child language transmission. With these ideas in place, it is possible to explore the further application of the RBN model to language, in particular to the transmission of languages across generations in a community. This is done in a quite idealized way here, as if the only input to a child learner is from a single adult. At the level of abstraction at which we are working here, this seems unlikely to be a harmful idealization. We go through the following steps:

• Specify an adult net by (randomly) generating a set of connections and activation functions.
• Specify the child net as having the same connections and activation functions as the adult. Thus we now have models of two individuals, `adult' and `child', with the same genetically specified expectations as to the set of languages they can learn, or `L.A.D. genotype'<sup>2</sup> (attractors they can gravitate to).
• Run the adult net from a random initial state (with all nodes set to either 1 or 0) until it reaches an attractor. This models the initial acquisition of a language from perfect data (an unrealistic assumption, but see below) by one individual, whose incomplete language performance will become the model for the subsequent acquisition of a language by its `child'.
• Set the child's initial net to a subset of one of the states in the attractor reached by the adult, the unset nodes being left as `?'. This step takes one state in the attractor reached by the adult as laying the basis for the language performance of the adult, but provides that the adult's performance will in fact only exemplify a subset of its grammar to the child, thus modelling the Poverty of Stimulus. `Cultural' transmission of language to the child is partial. The examples given to the child constitute what in the Chomskyan literature is referred to as the `Primary Linguistic Data' (PLD). At this point, one can specify what proportion of the adult's language gets exemplified explicitly to the child, i.e., how many of the nodes in the child's initial state are set to 1 or 0, with the rest left as `?'.
• Run the child's net until it reaches an attractor. This models the child's acquisition of its language from incomplete data, as illustrated earlier.
• Check whether or not the child's attractor is the same as the adult's. If the child's acquired language (the attractor the child net has gravitated to) contains any states with nodes still set to`?', then the child will not have acquired the adult's language faithfully, as the adult language had all states set to either 1 or 0. If the child's eventual attractor contains no states with any nodes set to `?', then the child has partially `reconstructed' the language, using `innate' knowledge.

Variable parameters of the model. For the purpose of experimenting with this model, certain parameters can be set to alternative values.

• N (the number of nodes in a net). Practical computing constraints mean that experimenting with high values of N is excessively time-consuming.
• K (the number of connections into each node). Again, high values of K impose processing limitations, but in fact values of K over about 5 tend all to give similar (typically chaotic) results. K can be variable; that is different nodes could have different numbers of incoming connections.
• Method of generating connections and functions --- random or hand-fixed. We will show how a net-specification, in terms of its connectivity and activation functions, can be hand-built to approximate to a realistic language-acquisition situation. Of further interest is the question of whether or not, with a population of initially random connectivities and activation functions, a realistic language-acquisition situation can be made to evolve, in an evolutionary algorithm.
• Method of degrading an adult state to give PLD probabilistic or fixed. A very crude simplifying assumption about the data presented to a child learner is that certain designated features of a language are always exemplified reliably in the primary linguistic data. More realistic is the assumption that certain features tend statistically to be exemplified more than others, probably with a Zipfian distribution, in which the most frequently exemplified feature is twice as likely to be exemplified (in a given utterance) as the second-most frequently exemplified feature, and so on.

A human-like net? It is possible to hand-tailor a net in such a way that the `adult' net gravitates to a wide variety of different attractors, and the `child' net reliably manages to gravitate to the same attractor as the adult, after initialization with incomplete data from the adult attractor. I give an example below.

• N = 200
• 15 specified nodes were self-connected, with a copying function [0 1]. Thus these nodes take input only from themselves, and once set, never change their values.
• The remaining 185 nodes were connected randomly (K = 2) to the 15 specified nodes, with random activation functions. That is, each of these 185 nodes takes input from some arbitrary pair of the 15 specified nodes, and gets activated according to a random Boolean function of the values of those nodes.

A schematic diagram might make this clearer.
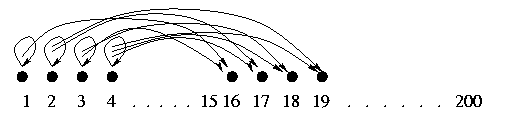
Fig. 1. Hand-made net with 15 self-connected nodes and 185 nodes taking two inputs each from nodes chosen randomly from the 15 self-connecting nodes.

This net was run 1000 times, from random initial states. In the child's PLD (the initial state), values of the 15 specified nodes were copied from a state in the adult attractor, and all 185 other nodes set to `?'. The results were as follows:

984 distinct adult attractors
984 distinct PLDs
984 distinct acquired attractors
1000 faithful acquisitions
Results with K = 3, 4, 5, 6 were essentially the same. This models substantial diversity of learnable languages and fidelity of transmission between generations.

But the method of degrading the input data used above is implausibly rigid. Another experiment was carried out, using probabilistic PLD-production. Here, the nodes were deemed to be rank-ordered by frequency; thus node 1 was deemed the most frequent, and node 200 the least frequent in use. Then the probability of a node in the child's initial state being set to 1 or 0 (as opposed to being left as a `?') was an inverse function of its frequency ranking. The probability of a node being set to 1 or 0 is given in the following graph:

Fig.2. Probabilistically distributed primary linguistic data. The probability with which nodes in the learner's trigger input are set to 1 is very high for a few nodes, and declines for the rest.

With this probabilistic input, the following results were obtained:

200 distinct adult attractors
200 distinct PLDs
200 distinct acquired attractors
182 faithful acquisitions
This achieves slightly better diversity of learnable languages, and slightly worse fidelity of transmission between generations.

Can such ``good'' nets be bred? It has been shown here that a Boolean net can be constructed by hand which, given the interpretation proposed, approximates reasonably well to a human language acquirer, in respect of the range of learnable languages, the fidelity of learning, the stability of the acquired state, and so forth. Chomsky's position on the human language capacity is that it is biologically given, and yet unlikely to have been specifically selected for by natural selection. I have briefly tested these ideas by trying to `breed' a particular net specification (in terms of connectivity and activation functions) with an evolutionary algorithm. In this algorithm, a net is specified in terms of a list of `genetic' loci, each allocated an allele from an available range. For instance, the alleles at one locus might code for the nodes from which node 17 receives its input; the alleles at another locus would code for the activation function of node 17. Each net in a population of nets is specified by a complete genome. The population size varied from 25 nets to 100, depending on the experiment. In the experiments, a heterogeneous population of nets with initially random connectivity and activation functions was evaluated according to a fitness function that rewarded for ability to acquire several different languages faithfully. Each generation, the more successful nets according to this fitness function were bred, and some mutation of the connectivity and activation functions took place. Selection was by tournament selection among groups of four. So far, the results have been negative. It has not been possible to `breed' a random Boolean net that performs as well, in terms of diversity of learnable languages and fidelity of intergenerational transmission, as the hand-fixed net described above. This may result from Boolean nets inhabiting a rugged fitness landscape, in which adaptation is unlikely. And it may possibly, upon further investigation, tend to confirm the Chomskyan view that the human capacity for language acquisition is not the result of natural selection. No such conclusion can yet be firmly drawn, however, because this paper has not exhausted all possible ways of identifying a dynamical system with the language organ, or of successfully creating such a system through an evolutionary process.

Endnote

1. See Koerner's 18-page chapter (Koerner, 1999:183-202), discussing various attributions, including to de Saussure and Meillet, but not managing to track down a convincingly original source of this bon mot.
2. L.A.D. stands for `Language Acquisition Device', an innate `mental organ' posited by Chomsky to explain the feat of language acquisition.