 1
1  2
2  2+1
2+1  2+2
2+2  5
5  5+1
5+1 Yareba7
 1
1  2
2  3
3  2+2
2+2  5
5  5+1
5+1 Korafe8
 1
1  2
2  2+1
2+1  4
4  5
5  5+1
5+1 Hunjara9
 1
1  2
2  2+1
2+1  2+1+1
2+1+1 Fuyuge (`Mafulu')10
 1
1  2
2  2+1
2+1  2+2
2+2  2+2+1
2+2+1  2+2+2
2+2+2
 2+2+2+1
2+2+2+1  2+2+2+2
2+2+2+2  2+2+2+2+1
2+2+2+2+1
(This is a version of a chapter in
Numeral
Types and Changes Worldwide, (Trends in Linguistics, Studies and
Monographs 118), edited by Jadranka Gvozdanovic. Mouton de Gruyter,
Berlin. pp.7-41.
Note: This HTML version may differ slightly from the printed
version; the printed version is the `authorized' version.)
A special kind of language change, not centrally studied in historical linguistics, is language growth. Growth is change from a smaller system (or perhaps even from nothing) to a larger system. Grammatical growth can occur by addition of lexical items or, perhaps more interestingly, of rules.
This paper describes attempts to simulate the growth of natural language numeral systems by computational techniques. Similar techniques could in principle by used to model the growth of other subsystems of grammar, and a long-term aim of this strand of research is to model the evolution of many of the organizational features of language. There are two salient factors in favour of using numeral systems as a test bed for this approach, and one salient factor against.
These properties of numeral systems are known well enough to need no further elaboration here.
The research paradigm inspiring this work is that of Artificial Life (`A-Life'). Two very readable popular introductions to this field are Levy (1992) and Lewin (1993), and there are now major collections stemming from workshops and conferences (Langton et al, (1991, 1994), Brooks and Maes (1994)).
Although terminologically reminiscent of the discipline of Artificial Intelligence (AI), A-Life differs from it in several fundamental philosophical and methodological principles. Whereas AI attempts to model developed or mature intelligence, the products of millennia of evolution, A-Life attempts to model the evolutionary processes leading to such products. AI systems are typically architecturally complex, embodying the programmer's analysis of the particular manifestation of intelligence under study (such as chess, parsing, visual processing, face recognition). A-Life systems are often, by comparison, architecturally simple, populated in a homogeneous structure by model individuals with (initially) very simple internal structures. In an AI system, the programmer maintains control of as many events in the computational process as possible, little or nothing being left to chance; in an A-Life system, the programmer defines boundary conditions for the evolutionary processes being modelled, and `sits back' to watch the interplay of random currents. AI typically models the behaviour of a single agent, whereas A-Life typically models multi-agent systems, in which many individuals interact in evolving populations. A-Life, being concerned with complex adaptive systems in general, is broader in its scope than AI, which is restricted to systems to which one can plausibly attribute intelligence.
Some classic examples of (relatively easily understood) seminal, though not necessarily typical, work in the spirit of A-Life are Conway's `Game of Life' (Garfinkel, 1983; Seife, 1994) and Ray's `Tierra' program (Ray, 1991a,b). Both these systems illustrate how the application of very simple principles over many `generations' can give rise to entities of remarkable complexity. Many of the evolved entities, moreover, show behaviour that can be interpreted as life-like.
Conway's Game of Life is played out by shapes defined by shading squares on graph paper. These change their outline every cycle by simple rules dictating whether squares adjacent to shaded squares get shaded or not, and whether shaded squares stay shaded. Some simple configurations oscillate between two shapes; some shapes effectively glide across the graph paper by changing like a snail's foot. Still more complicated configurations spawn such `gliders', giving rise to waves of offspring shapes, and some configurations are capable of self-replication. All of this is a surprise, or was to its fascinated discoverers (see Levy (1992) and for accounts).
Ray's Tierra system grows whole life-like eco-systems in the guts of a computer. Original minimally complex structures are defined in terms of configurations of addresses in core memory. Individual instantiations of such structures are `nourished' by the consumption of computing time, for which they have to compete by carrying out certain actions. If they don't get enough nourishment, they `die', that is they are removed from the arena of the computation. These `organisms' are also capable of self-replication, with the possibility of random mutations affecting the definition, in terms of core memory configurations, of the offspring. Allowed to run for many thousands of generations, Ray's Tierra systems evolve populations of diverse `species', which resemble ecological types in nature, such as parasites and predators. Every so often, there can be a wave of mass extinction, parallel to that evidenced by the real fossil record. The Tierra organisms are reminiscent of computer viruses, the most familiar form of artificial life.
The interest in such work, and in the many more specialized and perhaps less `toy' projects that have succeeded them, is in general in the emergence of complexity and order, in often in particular in the modelling of the evolution of complex natural systems by basic Darwinian principles from simple beginnings. The thought inspiring the present work is that (the grammars of) languages are complex naturally occurring systems, and one wonders to what extent techniques from A-Life research can be used to model their growth.
The differences between AI and A-Life sketched above are no doubt starkly simplified, but they give a true flavour of the methodological differences between the two approaches. One might further guess that whereas AI is more `application-driven' (good AI vision systems can be incorporated into useful robots; good parsers can be incorporated into useful machine-assisted translation programs), A-Life is more `curiosity-driven'. To an extent this is true, but it is now being discovered that some practical problems are so complex that broadly evolutionary, self-organizing, styles of system, in which programs are left to evolve their own solutions, are beginning to be viable in applied fields.
One particular technique in the wider A-Life armoury is Genetic Algorithms (GAs). See Koza (1992), Davis (1991), Goldberg (1989) and Holland (1975) for introductions to Genetic Algorithms. GAs mimic the biology of sexual reproduction. In sexual reproduction, the genes of both parents are randomly mixed; if there is much difference between the parents' genes, the genotype of the offspring will differ from that of both parents and will probably be a new genetic mixture unique in its population. The offspring will also differ from others in the population in the probability of its surviving and reproducing.
Evolving a working computer program by GA involves defining:
Clearly, in the expression `Genetic Algorithm', the term genetic is used metaphorically. The similarity between GAs and biological genetics is formal. GA's work because they exploit the same basic mechanisms of selection as biological evolution; the mechanisms themselves, abstracted away from the material on which they operate (say DNA), and the environments in which they are embedded (say the physical world), can be applied to try to model the evolution of any kind of complex adaptive system. It should be clear that GAs may not only model biological evolution, but many different manifestations of evolution, including, for example, the cultural evolution of social conventions. The key elements are selection, innovation by random mixing of the basic `genetic' units (whatever they may be, e.g. genes or memes), other random innovation (e.g. by biological mutation or small individual acts of cultural invention), faithful transmission of the `genetic' units between generations, and `superfecundity' (i.e. having a wide range of choices from which to select).
The experiments described later in this paper apply GAs to grammars, sets of lexical entries and phrase structure rules, which progressively evolve to express a greater range of meanings (numbers in this case) with maximal coverage, minimal redundancy, and maximal economy of expression.
If a computational system can be host to the evolution of naturalistic grammars, resembling the grammars of known languages, without the rules being directly invented and simply written in by the programmer, then presumably the system must in some sense be emulating the forces which gave rise to the real grammars of languages. The cautionary phrase `in some sense' is to be emphasized. Objects built of metal may always lack some of the properties of objects built of protein, but neither should possible similarities and parallelisms be ignored.
If naturalistic grammars can be evolved in a computer system, the parameters of the system in which this is done may be argued to shed light on the real-world conditions in which real grammars evolved. The grammars of individual languages are not themselves biological objects. The conditions that give rise to grammars are in part biological and in part social. Grammars are shaped both by the innate biological capacities of humans and by the pressures of the social environment. Some of the parameters of a computer system in which life-like grammars arise could be plausibly interpreted as mirroring bio-psychological capacities of individuals; and other parameters can plausibly seen as parallel to social forces operative in the `Arena of Use'2
If, however, repeated attempts fail to construct an artificial system in which grammars simply evolve, then there would be mounting evidence that natural grammars do not arise merely by the interaction of selection, random innovation and faithful transmission across generations. What might an alternative source of grammars be? Presumably something like a creationist account is the alternative to evolution, some kind of deliberate, one-off, large scale invention, masterminded perhaps by some genius. Such an account would see the grammar of a language as something analogous to Esperanto or perhaps Euclid's geometry , a whole integrated system springing fully formed from the brow of its inventor, and preserved but scarcely improved by succeeding generations over millennia.
The issue addressed could be expressed as: Did humans (somewhat deliberately) make language? or did language just grow in humans (and human societies)? The more one tries to flesh out any non-evolutionary explanation of how languages got to be the way they are, the less plausible any creationist or macro-inventionist account seems. Yet on the other hand, the evolutionary style of explanation, which holds that (the grammars of) languages evolved gradually into their present shapes, itself stands sorely in need of fleshing out. It remains to be demonstrated in detail that there could be plausible sets of conditions from which classical evolutionary mechanisms produce grammars of the familiar sort.
Defining and adjusting the parameters of a GA in which naturalistic grammars evolve provides a strictly disciplined framework within which the detailed conditions giving rise to linguistic evolution can be explored. Putting the matter at its least pretentious, all a GA does is emulate a fitness-driven random search of some space. The search space is defined by the properties of the basic genetic units, and the more or less complex configurations into which they may be combined. The strategy guiding the search is defined by the fitness function which selects the more promising configurations for `survival' and `reproduction' with each generation.
A specific example, simulating the growth of numeral systems, will be provided in the next sections, after which some due reservations about the complete appropriateness of GAs to the linguistic case will also be set out.
In this paper, we necessarily set rather humble goals, and concentrate on the cardinal numeral subgrammars of languages. What, then, are the numeral systems of languages like? It suits our purpose to distinguish between two broad types, which I will call `primitive' and `developed'. Naturally, there are some intermediate cases between primitive and developed, but the broad dichotomy is useful. I will characterize the two types of system in the next two subsections.
Not all languages have a numeral system. Some languages have quite simple systems, capable of counting only to about 20 or even lower. In primitive systems, the words have not always fully lost their non-numerical meanings. So the word for 5 might also mean `(left) hand'; the expression for `+ 1' might also mean `and another'; the expression for 10 might also mean `man' or `whole' or `finished' or `right hand'. In what follows, I will only mention the numerical meanings.
In these systems, either all the numeral expressions are monomorphemic (or at least do not contain more than one morpheme with a numerical interpretation), or a relatively low number, such as 2, 3, 4, or 5, is used as a basis of addition (or very much more rarely of subtraction or multiplication). Sometimes, after a base number appears in the counting sequence, it is used for all higher numbers. But this is not always so, and there can be what appears to be fairly random interspersing of morphologically complex numerals with monomorphemic numerals.
Examples of the first few numerals in some such simple systems are given below (in some cases, the examples given apparently comprise the whole system). In these examples, a single Arabic digit indicates that the number in question has an arithmetically simple, often monomorphemic, numeral; and where several Arabic digits are given, this indicates an arithmetically complex numeral, typically reflecting addition. Only a single example of each type is given here, but most of the types are not uncommon; more examples of them could be given, and from more than one part of the world. These primitive types are widely documented and discussed in a number of works surveying numeral systems (such as Conant (1923), Hymes (1955), Kluge (1937-42), Lean (1985-6), Menninger (1969), Pott (1847), Salzmann (1950), Seidenberg 1960).
Aomie6
 1
1  2
2  2+1
2+1  2+2
2+2  5
5  5+1
5+1
Yareba7
 1
1  2
2  3
3  2+2
2+2  5
5  5+1
5+1
Korafe8
 1
1  2
2  2+1
2+1  4
4  5
5  5+1
5+1
Hunjara9
 1
1  2
2  2+1
2+1  2+1+1
2+1+1
Fuyuge (`Mafulu')10
 1
1  2
2  2+1
2+1  2+2
2+2  2+2+1
2+2+1  2+2+2
2+2+2
 2+2+2+1
2+2+2+1  2+2+2+2
2+2+2+2  2+2+2+2+1
2+2+2+2+1
Mawae11
 1
1  2
2  3
3  3+1
3+1
 5x1
5x1
Tunisian Arabic egg-counting12
 1
1  2
2  3
3  4
4
 4+1
4+1  4+2
4+2  4+3
4+3  4x2
4x2
 4x2 +1
4x2 +1  4x2 +3
4x2 +3  3x4
3x4  ...
4x4
...
4x4  ... 5x4
... 5x4  ...
...
Motu13
 1
1  2
2  3
3  4
4  5
5  2x3
2x3  7
7
 2x4
2x4  2x4 +1
2x4 +1
Roro14
 1
1  2
2  3
3  4
4  5
5  2x3
2x3  2x3 +1
2x3 +1
 2x4
2x4  2x4 +1
2x4 +1
Keapara, Hula dialect15
 1
1  2
2  3
3  4
4  5
5
 2x3
2x3  2x4 -1
2x4 -1
 2x4
2x4  10-1
10-1
Hymes (1955:27) calls this type `pairing'; this pairing type, and several of the other types illustrated above and below, are found in Athabaskan languages, according to Hymes' survey.
Ekoi (Cameroun)16
 1
1  2
2  3
3  4
4  5
5  3+3
3+3  4+3
4+3  4+4
4+4  5+4
5+4
Onjob17
 1
1  2
2  3
3  4
4  5
5  5+1
5+1  5+1+1
5+1+1  5+1+2
5+1+2
 5+1+3
5+1+3  5+1+4
5+1+4
Miskito18
 1
1  2
2  3
3  2+2
2+2  5
5  5+1
5+1  5+1 +1
5+1 +1  5+1 +2
5+1 +2  5+1 +3
5+1 +3  5x2
5x2  5x2 +1
5x2 +1  5x2 +2
5x2 +2  5x2 +3
5x2 +3
 5x2 + 2+2
5x2 + 2+2
A purely 5-based system is referred to as `quinary'. Such systems are
very common, being found in almost all quarters of the world, and taking
the shape:
1  2
2  3
3  4
4  5
5  5+1
5+1  5+2
5+2
 5+3
5+3  5+4
5+4  10
10
The most familiar type of numeral system in better known languages is decimal, and sometimes also partly vigesimal. This canonical type has the following characteristics:
Examples of such systems are very familiar.
Further characteristics, common to both primitive and developed types of system, are:
We now bring the artificial techniques of Genetic Algorithms to bear on this diverse range of naturally occurring systems. The basic idea of GAs is applied here to grammars; the genetic units making up each `organism' are rules, which may be specifications of lexical items or rules of syntactic combination; each grammar is a set of such rules. The proposal is to selectively `breed' grammars of numeral systems from an initial randomly generated set of grammars. The interest is in seeing whether the range of systems described above simply emerges after systematic selection of grammars over many generations.
The elementary components of the system, by which rules are defined, are:
An arbitrary rule in the system is generated by taking the following steps, in order:
 s1
s1  fa (3)
fa (3)
 s2
s2  s1 s2 (addition)
s1 s2 (addition)
A grammar is a set of lexical items and phrase structure rules, of the sort just illustrated above. For numeral systems at least, this simple view of what constitutes a grammar is arguably adequate. A random grammar is a random-sized set of randomly generated lexical items and rules.
The core routine of the simulations carried out consisted of the following steps:
Implementing this system in detail calls for a number of decisions to be made. It is a virtue of the computational approach that it forces one to specify explicitly many parameters of grammars which are seldom, if ever, contemplated by descriptive linguists, although they are nonetheless real, and in no way artifacts arising simply out of the approach. In some cases, one can make a plausible intuitive guess at an appropriate value for some parameter, and hold it constant; in other cases, one can use the computational system to experimentally manipulate the values of parameters, within an intuitively plausible range. The relative success with which such experimental settings lead to naturalistic grammars can be taken as evidence pointing to corresponding values in the real-world conditions in which natural grammars evolved. In yet other cases, unfortunately, the settings of parameters are determined by computational convenience, although in no case did it seem that such settings were very counterintuitive. The more salient parameters involved in the current simulations are mentioned below. The first paremeters mentioned are linguistic, having to do with the nature of grammars; the ones mentioned later are `population-genetic', having to do with the particular mechanics of GAs.
SOME TWEAKABLE PARAMETERS
A number of simulations were run, under different conditions. These are described in order of growing complexity.
In this simulation, the grammars consisted only of lexical entries. There were no phrase structure rules. This simple experiment teaches us a lesson about the fitness function which applies to all more complex simulations. Which should be paramount in the fitness function, coverage or lack of redundancy? Putting it in terms of real human numeral systems, does the optimal system (i.e. that type found most commonly in human languages)
Repeated simulations were run in which the fitness function always preferred a grammar generating expressions for the most numbers, regardless of how many such expressions it generated for each number. Only when the coverage of two grammars was equal was relative lack of redundancy invoked to discriminate between them, in favour of the grammar generating fewer expressions.
With this fitness function, there was never any convergence on a naturalistic numeral lexicon, with just one word for each of the numbers from 1 to 10.
Another set of simulations was run in which the fitness function was the reverse of that just described. In this case, lack of redundancy, rather than coverage, was paramount. The fitness function always preferred a grammar which had as few extra expressions as possible for each number, even if some other grammar actually provided expressions for more numbers. Only when two grammars had equally few expressions was the coverage of meanings invoked, so that the grammar with the greater coverage was, then, preferred.
In this case also, after many runs, there was no convergence on a naturalistic numeral lexicon with just one word for each number up to 10.
On brief reflection, it becomes obvious why these simulations do not work to produce language-like results. Large grammars, containing more lexical items, are more likely to cover more meanings; just as a longer sequence of throws of a die is more likely to have at least one throw landing on each possible value than a shorter sequence of throws. If the selection process always favours coverage, large grammars will be selected which have enough lexical items to cover all the possible values. Almost inevitably, such grammars will be massively redundant.
Conversely, if lack of redundancy is selected for, the preferred grammars will be those which manage to express meanings with only one expression each. Small grammars, containing fewer lexical items, are more likely to avoid generating several expressions for the same number; just as a shorter sequence of throws of a die is more likely to avoid repetitions than a longer sequence. But the price of selecting smaller grammars is that they almost inevitably lack some coverage of the set of possible meanings.
Now a third set of simulations was run, in which the fitness of a grammar was calculated from a combination of coverage and lack of redundancy. Simply, and no doubt crudely, the fitness of a grammar in this case was inversely proportional to the sum of the gaps in the number sequence and the number of redundant expressions. To give an example, imagine a grammar which happened to provide words for numbers as follows:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| do | mi | la | ti | ||||||
| re | fa | do | so |
Here there are 6 numbers unexpressed by any word (i.e. 6 gaps), and 4 superfluous words. The combined gap-redundancy score is thus 6+4=10. Grammars with lower gap-redundancy scores were favoured in the simulation.
In these runs, there was always convergence to a naturalistic lexicon with just one word for each number from 1 to 10. Sometimes this convergence waas achieved very quickly, once in as few as 5 generations. In other runs, convergence took as long as 200 generations.
The combined gap-redundancy fitness function took no account of homonymy, and occasionally a simulation converged on a numeral lexicon in which a single monosyllable happened to express more than one number. This homonymy is, as far as I know, never found in real numeral systems. Further simulations should also build homonymy-avoidance into the fitness function. As the method for doing this is straightforward, this line of investigation was not followed. (In the grammars that emerged in later simulations, the occasional instances of homonymy were tolerated; nothing rides on this, as far as I can see.)
In the more complex simulations described below, the fitness function was always some combination of coverage and lack of redundancy, sometimes with other factors as well.
In further experiments with versions generating only simple lexicons, the situation after initial convergence on optimal fitness was studied, to see whether this fitness is maintained for long stable periods. Both mutation rate and population size were `tweaked'. Clearly, too fast a mutation rate (e.g. every cycle) stirs up the pool of grammars too much, and optimal fitness is only reached sporadically, with many lapses. But also important is population size. With 20 initial grammars and 5 grammars selected each cycle, there was frequent lapsing from optimal fitness over time, with few periods of stable optimal fitness. With 100 initial grammars and 10 grammars selected each cycle, the situation improved considerably, with long stable periods of optimal fitness, but still the occasional lapse, which was almost always immediately recovered from. With this population size, a mutation rate of 1 mutation per 15 grammars bred was, impressionistically, slightly more stable than a rate of 1 per 5.
The lesson one quickly learns, if one did not know it before, is that there is an intractably large number of possible variables, both linguistic and non-linguistic, which affect the evolution of grammars in this framework. By no means all of the possible variations are mentioned here, for readability's sake. Anyone attempting to replicate these experiments will be (or become) aware of the vast number of theoretical possibilities. It is conceivable that the evolution of real grammars is in fact subject to a small number of real variables. The computational approach described here might in principle lead to the discovery of some very parsimonious `magical combination' of settings of a few variables, which give rise to naturalistic grammars. Alternatively, lack of progress in finding such a combination might suggest the conclusion that the evolution of real-life grammars is subject to a great many chance vagaries, both psychological and social.
In the next series of experiments, the random grammars could contain both lexical items and simple phrase structure rules, as described above.
In the weightings for these runs, the random generation of a
syntactic rule was made as probable as the random generation of a
lexical item. Many of these simulations converged on numeral systems
of a mathematically very elegant type, but a type which is quite
unnatural, in the sense of being unrepresentative of natural languages.
The systems arrived at were highly economical of both lexical and
syntactic resources. They also achieved complete coverage of the number
sequence up to any limit, sometimes with no cost in redundancy. One
such extreme outcome was:
 s1
s1  mi (1)
mi (1)
 s1
s1  s1 s1 (addition)
s1 s1 (addition)
This grammar generates a single structure for the number 1, as in
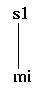
and a single structure for the number 2, namely
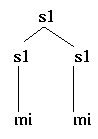
but at 3, (structural) redundancy sets in, with two possible structures
for 3, namely
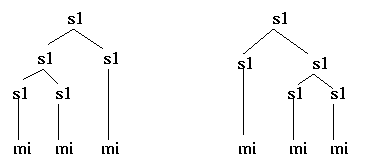
The redundancy increases dramatically as one proceeds to higher numbers. In the simulation that gave this result, only binary branching phrase structure rules had been allowed. Without the option of unary, or non-branching, phrase structure rules (or of binary rules which can include a simple lexical item, rather than a syntactic category, on the right hand side), there exists no grammar which can avoid this burgeoning redundancy.
With the possibility of unary, or non-branching, phrase structure rules,
a non-redundant grammar exactly parallel to Peano's axiomatic system for
defining the number sequence can arise, as follows:
 s1
s1  mi (1)
mi (1)
 s2
s2  s1
s1
 s2
s2  s2 s1 (addition)
s2 s1 (addition)
This grammar generates a single structure for each number, as shown
below for the numbers 1, 2 and 3:
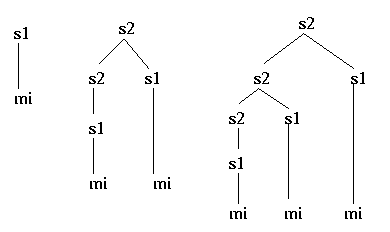
For the short term memories of humans, such a system is highly dysfunctional, and even self-defeating. The value of a counting system is in defining compact expressions which compress information. The psychological burden of counting the instances of the monosyllable mi in an expression for a higher number in this system renders it unusable. Such systems do not occur in spoken human languages. (But note the beginnings of such a system in written Roman numerals, I, II, III; such iconic representations of numbers can also be found in the ideographic cuneiform writing of the Sumerians and in Egyptian hieroglyphs.)
Such Peano-style grammars could result from various different combinations of circumstances. Factors which favour the evolution of such unnatural Peano-type solutions include:
One combination of variables was found to give rise to many systems closely resembling the natural `primitive' systems described earlier. Recall these were typically found in relatively small, and relatively isolated communities.
In these runs, a grammar's fitness was defined as the highest number it could 'count to' with no gaps, and not too much redundancy. Here, the algorithm to determine fitness is, basically: count from 1 upwards, and stop at the first gap, or where there are more than 2 (an arbitrarily chosen limit on redundancy) expressions for some number. The expected ratio of syntactic rules to lexical items was set at 1:8, and the number of abstract syntactic categories permitted was 2.
Starting with a population of 100 random grammars, the fittest 10 grammars were selected as parents grammars for the next generation. These parents bred (all with each other) a generation consisting of a further 100 offspring grammars. From this new generation, the fittest 10 were again selected as parents, and so on. The simulations ran for 1000 generations each, at which stage the fittest (usually the only) remaining grammar was inspected to see what numeral expressions, up to 20, it generated.
Of the 164 runs, over half (86) yielded lexicon-only solutions, summarized as follows:
| Words for numbers | Instances of this solution |
| 1 2 3 4 5 6 | 5 |
| 1 2 3 4 5 6 7 | 52 |
| 1 2 3 4 5 6 7 8 | 21 |
| 1 2 3 4 5 6 7 9 (gap at 8) | 4 |
| 1 2 3 4 5 6 7 8 9 | 3 |
| 1 2 3 4 5 6 7 8 10 (gap at 9) | 1 |
Such simple lexicons may perhaps be regarded as the basis on which somewhat more elaborate systems, with some syntactic rules, are founded.
In the remaining 78 runs, all solutions in some way resembled the natural primitive systems illustrated earlier. Solutions included base-2, base-3, base-4, base-5, base-6, and various mixed-base systems. Some examples are given below (note the occasional gaps and redundancies in these systems):
1 = 1
2 = 2
3 = 3
4 = [ 2 2]
5 = 5
6 = [ 2 [ 2 2]]
6 = [ [ 2 2] 2]
8 = [ [ 2 2] [ 2 2]]
1 = 1
2 = 2
3 = [ 1 2]
4 = [ 1 [ 1 2]]
5 = 5
6 = 6
7 = [ 5 2]
8 = [ 1 [ 5 2]]
8 = [ 5 [ 1 2]]
8 = [ 6 2]
9 = [ 1 [ 6 2]]
9 = [ 6 [ 1 2]]
12 = [ 5 [ 5 2]]
13 = [ 5 [ 6 2]]
13 = [ 6 [ 5 2]]
14 = [ 6 [ 6 2]]
1 = 1
2 = 2
3 = [ 2 1]
4 = [ 2 2]
5 = [ 2 [ 2 1]]
6 = [ 2 [ 2 2]]
7 = 7
8 = [ 7 1]
9 = 9
10 = [ 2 [ 7 1]]
10 = [ 7 [ 2 1]]
10 = [ 9 1]
11 = [ 7 [ 2 2]]
12 = [ 2 [ 9 1]]
12 = [ 9 [ 2 1]]
13 = [ 9 [ 2 2]]
14 = [ 2 7]
14 = [ 7 2]
15 = [ 7 [ 7 1]]
16 = [ 2 [ 2 7]]
16 = [ 2 [ 7 2]]
17 = [ 7 [ 9 1]]
17 = [ 9 [ 7 1]]
18 = [ 2 9]
18 = [ 9 2]
19 = [ 9 [ 9 1]]
20 = [ 2 [ 2 9]]
20 = [ 2 [ 9 2]]
1 = 1
2 = 2
3 = 3
4 = [ 1 3]
5 = [ 2 3]
6 = [ 3 3]
7 = [ [ 1 3] 3]
8 = [ [ 2 3] 3]
9 = [ [ 3 3] 3]
10 = 10
11 = [ 1 10]
12 = [ 2 10]
13 = [ 3 10]
13 = [ 10 3]
14 = [ [ 1 3] 10]
14 = [ [ 1 10] 3]
15 = [ [ 2 3] 10]
15 = [ [ 2 10] 3]
16 = [ [ 3 3] 10]
16 = [ [ 3 10] 3]
16 = [ [ 10 3] 3]
20 = [ 10 10]
1 = 1
2 = 2
3 = 3
4 = 4
5 = 5
6 = [ 3 3]
7 = [ 3 4]
7 = [ 4 3]
8 = [ 3 5]
8 = [ 4 4]
8 = [ 5 3]
9 = [ 4 5]
9 = [ 5 4]
10 = [ 5 5]
1 = 1
2 = 2
3 = 3
4 = 4
5 = [ 1 4]
6 = [ 2 4]
7 = [ 3 4]
8 = [ 4 4]
9 = [ [ 1 4] 4]
10 = [ [ 2 4] 4]
11 = [ [ 3 4] 4]
12 = [ [ 4 4] 4]
1 = 1
2 = 2
3 = 3
4 = 4
5 = [ 4 1]
6 = [ 4 2]
7 = [ 4 3]
8 = 8
9 = [ 4 [ 4 1]]
10 = [ 4 [ 4 2]]
11 = [ 4 [ 4 3]]
12 = [ 4 8]
16 = [ 4 [ 4 8]]
1 = 1
2 = 2
3 = 3
4 = 4
5 = 5
6 = [ 5 1]
7 = [ 5 2]
8 = [ 5 3]
9 = [ 5 4]
10 = 10
11 = [ 5 [ 5 1]]
12 = [ 5 [ 5 2]]
13 = [ 5 [ 5 3]]
14 = [ 5 [ 5 4]]
15 = [ 5 10]
20 = [ 5 [ 5 10]]
1 = 1
2 = 2
3 = 3
4 = 4
5 = 5
6 = 6
7 = [ 6 1]
8 = [ 6 2]
9 = [ 6 3]
10 = [ 6 4]
11 = [ 6 5]
13 = [ 6 [ 6 1]]
14 = [ 6 [ 6 2]]
15 = [ 6 [ 6 3]]
16 = [ 6 [ 6 4]]
17 = [ 6 [ 6 5]]
The similarities between these artificially generated systems and the `primitive' systems described earlier, are striking.
It is noteworthy that, of all the artificial grammars generated in the runs described above, not a single pure decimal system emerged. We will explore why this is so.
Recall that what is simulated here is a quasi-social process whereby grammars are formed from a pool of variant lexical items and syntactic rules which are somehow ambient in the community. Over time, the pool of available lexical items and rules becomes restricted so that only one grammar may be constructed from them, and this grammar is the `fittest' that the community has happened upon. After that point of convergence, only random `mutations' to the pool of lexical items and rules may disturb the situation. And such mutant lexical items or rules will only persist in the pool if they happen to fit in with existing rules and lexical items to form a grammar which is fitter than the one previously converged upon.
As readers familiar with any complex adaptive system will know, there can exist many `local optima', that is solutions to a problem (such as finding an effective counting system) which are fitter than their close neighbours in the possibility space, but not the fittest solutions overall, in any global sense. It is clear that the artificial systems illustrated above are local (near-)optima, in this sense. In other words, any small mutation to one of the grammars arrived at tended very strongly to produce a grammar that was less fit
If a particular grammar converged upon by the algorithm is at a local optimum, then any random mutation applied to it, in the form of a randomly added or deleted syntactic rule or lexical item, will result in a grammar less fit (by whatever definition of fitness was used to arrive at the tested grammar) than the tested grammar. If such random mutations do not always, but nevertheless tend strongly to, result in less fit grammars, then the tested grammar is near a local optimum.
The 13 first grammars converged upon by the algorithm decribed above were tested for local optimality in this way. To each of these grammars, 100 random mutations were applied (not serially, but always starting with the tested grammar). Thus for each tested grammar, 100 one-step mutants were produced. The results for the 13 tested grammars are aggregated below.
| 1 mutation produced a less fit grammar | in 444 cases. |
| 1 mutation produced an equally fit grammar | in 776 cases. | in 80 cases. |
Thus the probability of a random mutation producing an improvement to one of the converged-upon grammars is low, 0.062 (80/1300). These grammars are at or near local optima.
To test whether the algorithm would recognize a globally optimal solution if it saw one, another series of runs was carried out in which the initial population of 100 random grammars was `seeded' with a small number (10) of copies of a grammar which (I thought) was globally optimal. There were no nasty surprises here, and the algorithm always quickly converged, after just one or two cycles, on the globally optimal solution. The algorithm did however administer one sobering little lesson, in that it discovered a better grammar than the one with which I had seeded it. My `optimal' grammar was not quite optimal, as it allowed both 1-deleted and non-1-deleted variants of 10 (i.e. 10 = 10 and 10 = 1x10), which occurred in all the -teen expressions, giving redundancy.
The algorithm explored here never succeeded, in a limited number of trials, in converging on a complete and pure decimal numeral system such as is the basis of the counting systems of most of the world's major languages. On several occasions it got close. One its better efforts was as follows:
LEXICON:
| Value | Syntactic Category | Word |
|---|---|---|
| 1 | s0 | re |
| 2 | s0 | ga |
| 3 | s0 | ko |
| 4 | s0 | se |
| 5 | s0 | ji |
| 6 | s0 | ge |
| 7 | s0 | ci |
| 8 | s0 | ti |
| 9 | s0 | le |
| 10 | s2 | di |
SYNTACTIC RULES
 s0
s0  s2 s0 (addition)
s2 s0 (addition)
 s1
s1  s2 s2 (addition)
s2 s2 (addition)
COMPLEX EXPRESSIONS GENERATED
11 = 10+1
12 = 10+2
13 = 10+3
14 = 10+4
15 = 10+5
16 = 10+6
17 = 10+7
18 = 10+8
19 = 10+9
20 = 10+10
As can be seen, this system is like a developed decimal system up to 20, but goes no further.
Another near miss (though at first blush it may not look like it) is as follows:
1 (GAP)
2 = 2
3 = 3
4 = 4
5 = 5
6 = 6
7 (GAP)
8 = 8
9 = 9
10 = 10
11 (GAP)
12 = 10+2
13 = 10+3
14 (GAP)
15 (GAP)
16 = 10+6
17 (GAP)
18 = 10+8
19 = 10+9
20 = 2x10
21 (GAP)
22 = 2x10 + 2
23 = 2x10 + 3
24 (GAP)
25 (GAP)
26 = 2x10 + 6
27 (GAP)
28 = 2x10 + 8
29 = 2x10 + 9
31 (GAP)
32 = 3x10 + 2
33 = 3x10 + 3
34 (GAP)
35 (GAP)
36 = 3x10 + 6
37 (GAP)
38 = 3x10 + 8
39 = 3x10 + 9
40 = 2 x 2x10
41-59 (GAPS)
60 = 2 x 3x10
 3 x 2x10
3 x 2x10  6x10 (REDUNDANCY)
6x10 (REDUNDANCY)
61 (GAP)
62 = 6x10 + 2
63 = 6x10 + 3
64 (GAP)
65 (GAP)
66 = 6x10 + 6
67 (GAP)
68 = 6x10 + 8
69 = 6x10 + 9
70-79 (GAPS)
80 = 8x10
81 (GAP)
82 = 8x10 + 2
83 = 8x10 + 3
84 (GAP)
85 (GAP)
86 = 8x10 + 6
87 (GAP)
88 = 8x10 + 8
89 = 8x10 + 9
90 = 9x10  3 x 3x10 (REDUNDANCY)
3 x 3x10 (REDUNDANCY)
91 (GAP)
92 = 9x10 + 2
93 = 9x10 + 3
94 (GAP)
95 (GAP)
96 = 9x10 + 6
97 (GAP)
98 = 9x10 + 8
99 = 9x10 + 9
The main problem with this system is the lexical gaps for values 1 and 7, and the gaps caused by the fact that the words for 4 and 5 are not of the appropriate syntactic category to fit into the higher-valued syntactic constructions. If those gaps were filled with appropriately categorized lexical items, the system would be close to a modern decimal system. But note the hint of a vigesimal system in the various ways of expressing 60.
In the artificial approach described here, a numeral system resembling the dominant type found in the world's languages can emerge only very rarely, though it is not actually impossible. On the other hand, `suboptimal systems', resembling the systems found in a number of isolated language communities throughout the world, emerge frequently. If a developed system is artificially imposed on a community with such a suboptimal system, the developed system is quickly adopted. If the approach outlined here has any verisimilitude, we may conclude that the natural primitive systems have an internal stability but are highly vulnerable to invasion (through language contact) by the developed decimal system which prevails throughout much of the world. This fits very well with the facts of language contact; in fact, `exotic' numeral systems as have been shown above are typically abandoned in favour of a `modern' decimal system. The simulations here show that this replacement may be due to some kind of real linguistic superiority (in coverage, lack of redundancy, and suitability to specifically human memory constraints) of the decimal system, and not just a consequence of the superior economic or military power of the invading culture.