A claim from Shannon (1948) is that communication can usefully be understood as information transmission over a capacity-limited noisy channel. Under that assumption, an optimal strategy (Levy & Jaeger 2007) in language production is to maintain a uniform rate of information transmission close to the channel capacity. This section considers the evidence for such a claim.
To start, let's consider how one might estimate information content. The intuition is that things that are surprising have high information content; things that are unsurprising have low information content. If one treats surprisal in terms of probability, then elements in language that appear often (that have a higher probability of appearing) are less surprising than elements that appear rarely (that have a low probability of appearing). It's a little trickier than this (see Entropy), but that intuition will suffice for the discussion below.
How would one estimate surprisal? Well, if we're working with a corpus, we can estimate the probability of a particular word by counting how often it occurs: Rare words are more surprising to encounter than frequent words. To get a bit more nuanced, word-level surprisal can also be estimated by taking into account the words that precede a particular word: A word may be surprising given the preceding bigram of words (e.g., "I eat dogs") or it may be unsurprising ("I love dogs"). These are called n-gram probabilities and are used to estimate n-gram surprisal.
If we're working with a parsed corpus (i.e., one that provides a syntactic tree for each sentence), we can estimate the probability of a particular structure by counting how it occurs: Rare structures are more surprising than frequent structures. Again to get a bit more nuanced, structural surprisal can also be conditioned on context: The particular structure of a verb's complement may be surprising given that verb (e.g., "know" can appear with a complement clause or a direct object but one might be more surprising than the other).
Let's now consider what behaviour we would expect within a sentence if the UID claim holds. First off, we might see lengthening of rarer words, which we do (Aylett & Turk, 2004).
Not only can individual words be lengthened but sentences can be lengthened via the inclusion of optional words. For example, there is a set of verbs which can either be followed by a direct object or by an embedded clause, as in (9) and (10).
(9) I know the right answer.
(10) I know the right answer may be hard to find.
Of the verbs in that family, some appear more with an embedded clause ("guess [clause]") whereas other verbs disprefer embedded clauses (favoring other arguments: e.g., "worry about the answer"). It's possible to insert the word "that" at the beginning of the embedded clause for both types of verb, as in (11) and (12):
(11) I guess that the right answer may be hard to find.
(12) I worry that the right answer may be hard to find.
What about across sentences? UID claim is that speakers optimise communication by maintaining a uniform rate of information -- a uniform rate of surprisal (or as close to uniform as possible). Compare (13) and (14). Both describe roughly the same event and use the same set of content words (species, discover, bog, University, etc.). However, (13) packs that information into 24 words whereas (14) spreads that information out across 30 words. The difference is largely in the number of function words ("a", "that", "has", "was", etc.).
(13) A new species of gecko was discovered last month at a bog by a young scientist from the University of Edinburgh's evolutionary biology lab.
(14) The University of Edinburgh has an evolutionary biology lab. That lab has a young scientist. That scientist was at a bog last month. She discovered a new species of gecko.
If we assume that encountering a content word is more surprising than encountering a function word ("bog" is much rarer in a corpus than "was"), then Y distributes the same set of high-information encounters over a larger number of words. This means that on average, the surprisal of a word in (14) is lower than it is in (13).
Genzel & Charniak (2002) considered the average surprisal of each word in a corpus of Wall Street Journal (WSJ) news text and found that as they moved from the beginning of a WSJ article to the end, the average surprisal increased. See figure 1 from their paper, where the x axis shows sentence number in a WSJ article and the y axis shows a measure of surprisal (up being more surprising):
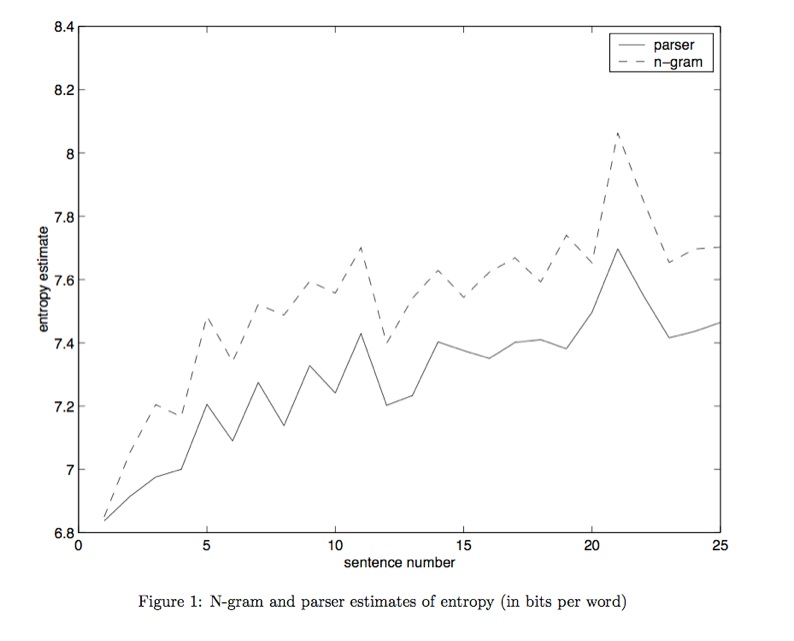
They also found that the average surprisal based on the syntactic parse showed an increase from the beginning of a WSJ article to the end. Can this observed increase in surprisal be reconciled with the UID claim? Yes. The reason being that the word-level and structural estimates of surprisal lack discourse context. Those estimates are local (how surprising is this word given the previous bigram, how surprising is this part of the tree structure given the preceding part of the tree structure). They are local because estimates of surprisal are computed over strings of text and parse trees, not over mental representations or pragmatic context. When humans (rather than computers) encounter a WSJ article, they can build up contextual knowledge over the course of the text. What this means is that the mention of a rare word or the use of a rare structure may not be as surprising if that word or structure has already been added to the common ground. If we consider (13) and (14) again, it seems more likely that (14) would be a gentler way to ease a reader into the topic (perhaps too gentle!)(i.e., maybe it fails to take advantage of the information capacity of the communication channel and is a little too plodding in doling out the information). Therefore (14) might be more likely to appear early in a text, at a point where the topics of scientific discovery and universities etc. are brand new to the reader. Once those notions are introduced, it is presumably easier on the reader to encounter a more information-dense packaging of related news about a similar event. Imagine if the text in (15) appeared later in the news article.
(15) That's not the only recent discovery. A new species of bird was discovered last week on a cliff by a rock climber from the University of Glasgow's outdoors club, and a new species of fish was discovered yesterday in a fjord by a fisherman from the University of Aberdeen's angler club.
By the time the reader gets to the underlined sentence in (15), they will likely have an easier time processing the content words like "species" and "discover" and "University" than they did the first time they encountered those words in the article. Likewise, the passive voice (a rarer structure than active voice) would likely be easier to process following a similar passive construction in the preceding clause. It is this discourse context that a human has access to (the words/concepts/entities that have already been mentioned and the linguistic structures that have already been used) that makes the computationally estimated increase in surprisal manageable. In this way, an increase in surprisal (Genzel & Charniak 2002) fits the UID claim. We know common ground increases over the course of a discourse, and if word-level and structural surprisal stayed constant, that would actually mean that the surprisal experienced by the reader would go down. Instead, the world-level and structural surprisal increases but the growing common ground mitigates its effects.
An interesting open question in this domain is why speakers adhere to UID. Is it for the benefit of their listener, whereby the speaker is engaging in some sort of audience design, making their utterance easier for the listener? Or do they do it merely for themselves because more effort is required for the retrieval/production of high-information material and that effort can be eased by distributing it across a longer duration. Even if speakers do make these adjustments entirely for themselves, there is nonetheless evidence that listeners take advantage of such lengthening. For example, a study by Jennifer Arnold (nicely named If you say thee uh you are describing something hard: the on-line attribution of disfluency during reference comprehension) shows that listeners who hear a speaker being disfluent are likely to guess (as evidenced by their eye movements) that the upcoming word refers to a novel difficult-to-describe object.
Lastly, if you're interested in UID, you can read more in this short 6-page conference paper (Frank & Jaeger, 2008) that discusses when and where speakers use contractions: Speaking Rationally: Uniform Information Density as an Optimal Strategy for Language Production.
Aylett, M., & Turk, A. (2004). The smooth signal redundancy hypothesis: A functional explanation for relationships between redundancy, prosodic prominence, and duration in spontaneous speech. Language & Speech, 47, 31-56.
Brennan, S. E. & Clark, H. H. (1996) Conceptual pacts and lexical choice in conversation. Journal of Experimental Psychology: Learning, Memory, and Cognition, 22, 1482-1493.
Gahl, S. 2008. "Thyme" and "time" are not homophones. The effect of lemma frequency on word durations in spontaneous speech. Language 84(3), 474-496.
Garrod, S. & Pickering, M. J. (2004). Why is conversation so easy? TRENDS in Cognitive Science, 8, 8-11.
Genzel, D., & Charniak, E. (2002). Entropy rate constancy in text. Proceedings of ACL–2002, Philadelphia, 199-206.
Horton, W. S. (2007). influence of partner-specific memory associations on language production: Evidence from picture naming. Language & Cognitive Processes, 22(7): 1114-1139.
Horton, W. S. & Keysar B. (1996). When do speakers take into account common ground? Cognition, 59: 91-117.
Horton, W. S. & Spieler, D. H. (2008) Age-related effects in communication and audience design. Psychology and Aging.
Jaeger, T. F. 2010. Redundancy and Reduction: Speakers Manage Syntactic Information Density. Cognitive Psychology, 61(1), 23-62.
Levy, R., & Jaeger, T. F. (2007). Speakers optimize information density through syntactic reduction. In B. Scholkopf, J. Platt, & T. Hoffman (Eds.), (p. 849-856). Cambridge, MA: MIT Press.
Shannon, C. E. (1948). A mathematical theory of communications. Bell Systems Technical Journal, 27, 623-656.